Annuity Future Value
Results
Future Value(Payment at Beginning):$15,816.95
Please note that the total payment over years is $12,000.00 and the total interest earned is $3,816.95
Description
This FutureValue of Annuity calculator helps you to calculate the value of a series of equal cash flows at a future date. You can use this calculator to find out how much money you will have in your savings account at a future date, if you deposit same amount money in every period and savings account adds a fixed interest to your account. Real world example of this is a fixed deposit or time deposit with a bank.
What is an Annuity
An annuity is a specialized financial arrangement involving a sequence of payments over a designated timeframe, regardless of the money's direction (incoming or outgoing). Annuities need to fulfill two conditions: the payments being uniform and occurring at regular intervals. For instance, $500 payments made at the end of each year of the upcoming ten years constitutes a 10 - year annuity.
Annuity Types
Annuities can be cla ssified in a variety of ways such as contingent annuity, guaranteed annuity, fixed annuities, variable annuities, and equity - indexed annuities. From the perspective of this annuity calculator, we differentiate annuities in terms the timing of the payments. There are two types of annuities:
Ordinary Annuity:
Payments are made at the end of the periods. Example of ordinary annuity are mortgages, car loans, and student loans.
Annuity due:
Payments are made at the beginning of each period. Example of annuity due are rental lease payments, life/health insurance premium, and lottery payoffs.
Formula to calculate future value of an annuity
The two basic annuity formulas are as follows:
FV of Ordinary Annuity
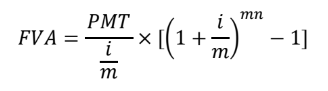 Where, PMT = periodic payment; i = annual interest rate; n = number of years; m = number of period in a year. For example, m=1 for annually; m=365 for daily; m=2 for semi - annually; m=4 for quarterly; m=12 for monthly.
Where, PMT = periodic payment; i = annual interest rate; n = number of years; m = number of period in a year. For example, m=1 for annually; m=365 for daily; m=2 for semi - annually; m=4 for quarterly; m=12 for monthly.FV of Annuity due
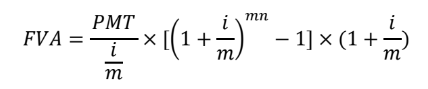 Where, PMT = periodic payment; i = annual interest rate; n = number of years; m = number of period in a year. For example, m=1 for annually; m=365 for daily; m=2 for semi - annually; m=4 for quarterly; m=12 for monthly.
Where, PMT = periodic payment; i = annual interest rate; n = number of years; m = number of period in a year. For example, m=1 for annually; m=365 for daily; m=2 for semi - annually; m=4 for quarterly; m=12 for monthly.How to use this annuity calculator ?
Lets assume that you want to save $ 1,200 in a savings account by the end of every year for 10 years. Bank agrees to pay you a 6 % interest on your savings account compounded every year. Now you want to know how much money you will have in your savings account in 10 years from today. The most important implication of this kind of calculation is the retirement savings account. Here is how you can use this calculator.
Periodic Payment Amount:
Enter $1,200 as your periodic payment amount. For example, a yearly payment of $1,200 will be $300 when paid quarterly. Your input should be greater than 0.
Payment Interval:
Select Annually if payment is made only once a year. Select daily if payment is made daily, and etc. This will be used as the basis of interest compounding.
Payment at..:
Select end (ordinary) if you make payment at the end of the period. Select beginning (due) if you make payment at the beginning of the period.
Annual Interest Rate:
Enter an annual interest rate of 6% if you think your account will earn interests at 6% annually. You are allowed to enter a minimum value of 0%.
Number of Years:
Enter 10 if you want to save money with an equal amount for 10 years in a row. In other words, this is your annuity duration. Your entered number has to be greater than 0.
Once you entered all the numbers as stated above, click on “Calculate” button. The calculator will show the future value of the annuity as $15,816.95.The total payment is $12,000.00 and the total interest earned is $3,816.95.