What is a Bond?

A bond is a fixed - income instrument that represents a loan made by an investor to a borrower (typically corporate or governmental). A bond could be thought of as an I.O.U. between the lender and borrower that includes the details of the loan and its payments. Bonds are used by companies, municipalities, states, and sovereign governments to finance projects and operations. Owners of bonds are debtholders, or creditors, of the issuer.

When you purchase a bond from the bond issuer, you are essentially making a loan to the bond issuer. As the bond price is the amount of money investors pay for acquiring the bond, it is one of the most important metrics in valuing the bond.

What is a Bond yield?

Bond yield, also often known as the yield to maturity (YTM), is often understood as the rate of return for bond investors, given that the bond investors hold the bond until it matures and reinvest the coupons at an interest rate equal to the YTM. As bond yield is very volatile and sensitive to the economic climate, it is of the essence that we understand its dynamics and calculation.

How to calculate Bond yield?

Bond yield calculation involves complex iteration, and it is nearly impossible to do it by hand. That’s why our calculator is built and make the calculation a lot easier. In our calculator, if you enter $965 as bond price, $1,000 as Face value, 5 % as the annual coupon rate, semi - annually as the coupon frequency, 5 years as the years to maturity or bond life , we can use the following equation and plug in the numbers to calculate bond yield . Specifically, in the equation below, the rate of return (r ) that makes left - hand side equal to the right - hand side of the equation is the yield to maturity or YTM.

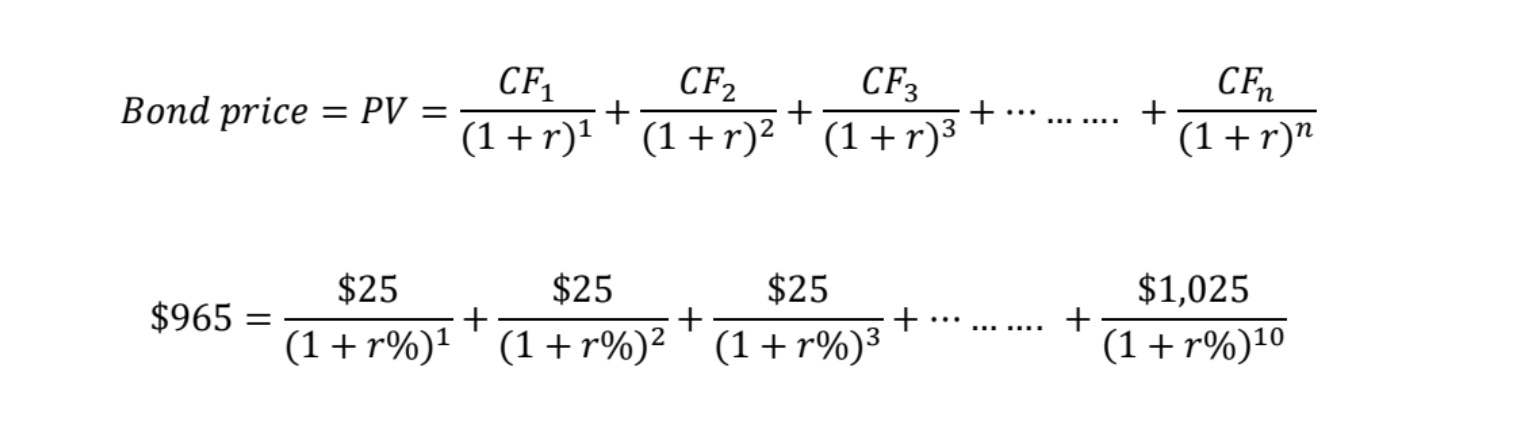
Now, if we solve for r%, we get a value of 5.82%, which is our YTM. In other words, if we calculate the PV of all future Cash Flows of the bond by using a discount rate of 5.82%, the bond value will exactly be equal to $965. Therefore, 5.82% makes the equ ation balanced.

Additionally, the current yield of a bond is the annual coupon payment in dollar divided by the bond price. In our example, we divide a coupon payment of $50 by $965 to get the current yield of 5.18%